Принципы компьютерной томографии
Математические методы синтеза изображений приобрели в последние годы столь большое значение в медицинской диагностике, что о них следует говорить особо. Применение ЭВМ в медицинской интроскопии для синтеза двумерных изображений из серии разноракурсных одномерных сигналов привело к настоящей революции в медицинской диагностике благодаря созданию и широкому внедрению в медицинскую практику нового класса интроскопической аппаратуры, который можно определить общим названием – вычислительные или компьютерные томографы.
Компьютерный томограф Хаунсфилда. G. Haunsfield. В 1973 г. группа английских инженеров во главе с G. Haunsfield разработала рентгеновский аппарат с ЭВМ для исследования головного мозга, назвав его «EMI-сканнером». EMI – аббревиатура названия фирмы «Electro Musical Instruments». Это был рентгеновский компьютерный томограф.
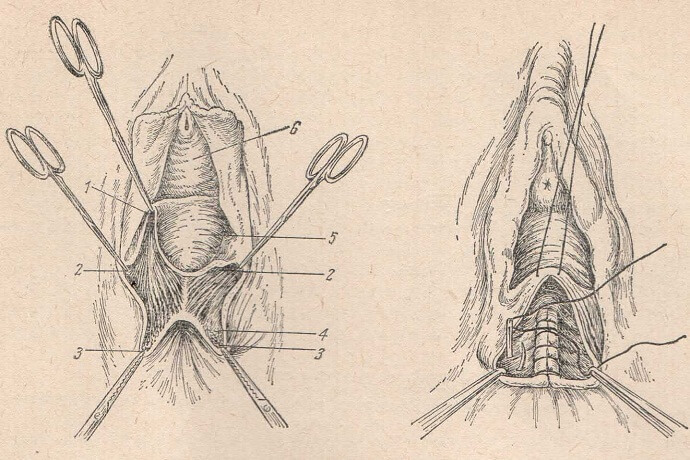
В томографе Haunsfield с противоположных от исследуемого объекта сторон синхронно перемещались точечный рентгеновский луч и детектор, «рассекая» объект поперек. Детектор все время регистрировал прошедшее через объект излучение. Затем система излучатель–детектор поворачивалась на несколько градусов относительно центра объекта и сканирование повторялось (рис. 61,а). Все последовательные сигналы детектора, квантованные с помощью АЦП, вводились в ЭВМ и обрабатывались по специальной программе, синтезируя двумерное рентгеновское изображение исследуемого слоя.
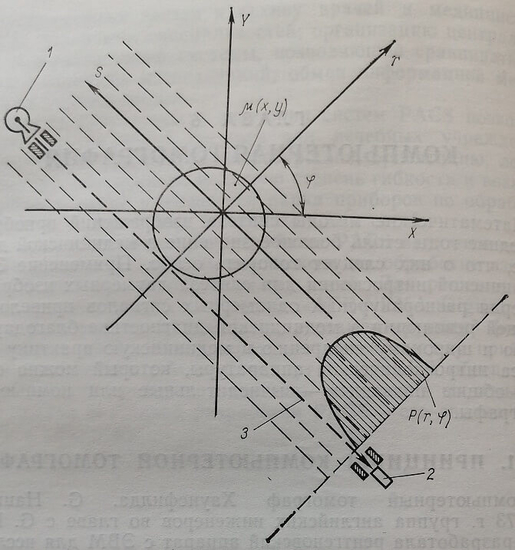
Рис. 61. Графическое объяснение перехода от прямоугольных к полярным координатам при реконструкции по линейным проекциям. 1 – рентгеновский излучатель; 2 – детектор; 3 – коллимированный луч
За прошедшие после изобратения G. Haunsfield 10 лет число рентгеновских компьютерных томографов, работающих в клиниках всего мира, превысило 10 000. Это совсем не мало, если учесть, что стоимость одного такого прибора составляла почти 1 млн долларов. В настоящее время с помощью компьютерного томографа производят исследование практически всех органов и систем человеческого организма.
Томографией (от греческого tomo – слой и graph – пишу) называют методику рентгенологического исследования, с помощью которой можно воспроизводить изображение слоя, лежащего на определенной глубине объекта. Обычный томографический снимок получают синхронно перемещая излучатель и рентгеновскую пленку в противоположных направлениях таким образом, чтобы тени органов, лежащих вне слоя, размывались при движении, а изображение слоя оставалось четким. Однако обычная томография эффективна лишь в случае объектов с высокими собственными различиями по рентгеновской плотности, например легких и костей, или органов, ставших непрозрачными благодаря введению контрастных веществ, как почки.
Методы получения обычного теневого изображения в традиционной диагностике основаны на прямом преобразовании потока энергии квантов рентгеновского излучения, прошедшего исследуемый объект, в видимое изображение на флюоресцирующем экране, рентгеновской пленке или другом носителе. Такие изображения имеют следующие недостатки: наложение изображений наслаивающихся структур, осложняющее идентификацию нормальных и патологических образований; разрешение по плотности не лучше, чем 2%; наибольший перепад плотностей,одновременно регистрируемых на изображениях без искажений составляет около 100.
Так как врача-диагноста интересуют именно малые отклонения плотности в объекте с большим диапазоном плотностей, а также как можно более точная локализация патологических изменений, то эти недостатки являются принципиальными. Компьютерная рентгеновская томография обеспечивает получение изображения поперечного слоя исследуемого объекта с помощью математической обработки множества рентгеновских изображений одного и того же поперечного слоя, сделанных под разными углами, восстанавливая двумерное изображение из серии одномерных. При этом главным и принципиальным отличием изображения в компьютерной томографии является то, что это изображение – результат точных измерений и вычислений, относящихся именно к выбранному слою.
Поэтому изображение в рентгеновской компьютерной томографии лишено перечисленных недостатков изображения традиционной диагностики, а именно, обладает почти в 10 раз большим контрастным разрешением во всем диапазоне изменения рентгеновских плотностей человеческого тела, делая возможным дифференциацию мягких тканей, позволяет разделять изображения наслаивающихся структур и точно показывать область патологических изменений. Несмотря на то что все остальные параметры изображения, полученного на вычислительном томографе (пространственная и временная разрешающие способности, геометрическая и динамическая нерезкости) уступают рентгенограмме, отмеченные преимущества оказались решающими для расширения возможностей рентгенодиагностики.
Принципы рентгеновской компьютерной томографии. Информацию о внутренней структуре исследуемого объекта в рентгенодиагностике несет пространственное распределение интенсивности рентгеновского излучения, прошедшего через этот объект.
В компьютерной томографии ЭВМ восстанавливает двумерное изображение объекта на основании многоракурсных одномерных сигналов детектора, пропорциональных 1(B). Геометрия облучения приведена на рис. 61. Рентгеновское излучение, проходя через объект, фильтруется и соответственно становится более жестким, поэтому коэффициент линейного ослабления однородного объекта будет уменьшаться по мере прохождения излучения через объект. Этот эффект называется «ходом с жесткостью» и должен учитываться при реконструкции изображения. Коррекция «хода с жесткостью» проводится с помощью однородного водного фантома, изображение которого просто вычитается из изображения исследуемого объекта. При этом используется близость линейного коэффициента ослабления воды и мягких тканей организма человека при эффективных энергиях излучения компьютерных томографов, как правило, лежащих в интервале 60–80 кэВ. Так, ц для мускульной ткани на 5% выше, а жировой на 10% ниже, чем ц воды. Белое и серое вещество головного мозга отличаются друг от друга на 0,5% и от воды на 3,5%.
Линейные коэффициенты ослабления удобно выражать в относительных единицах шкалы, которую ввел Хаунсфилд.
Нижняя граница шкалы –1000 соответствует ослаблению в воздухе, верхняя граница +1000 – ослаблению в костях, за нуль принимают коэффициент ослабления воды. EMI-сканнер Haunsfield работал при анодном напряжении 120 кВ, с алюминиевым фильтром 4,5 мм толщиной и калибровался с помощью водного фантома диаметром 27 см. Единица этой шкалы названа в честь создателя первого компьютерного томографа хаунсфилдом и обозначается латинской буквой Н.
Термин «компьютерная томография» вошел в употребление после изобретения Н. Haunsfield рентгеновского компьютерного томографа. Сейчас под компьютерной томографией понимают самые разные варианты методов реконструкции изображения и типов физических измерений, и все большее число способов измерений, применяемых в технике, может рассматриваться как разновидность компьютерной томографии. Сформулируем определение метода компьютерной томографии [70], введя несколько вспомогательных терминов:
- исследователь – тот, кто производит измерения с помощью метода компьютерной томографии;
- тело – объект, внутреннее строение которого изучается исследователем;
- воздействие – физический процесс произвольной природы (излучение, статическое поле и т. д.), служащий для исследования внутренней структуры тела;
- преобразователь – любой источник или приемник энергии (например, рентгеновская трубка и детектор) при условии, что он находится под контролем исследователя;
- система – сочетание аппаратуры, измерительной схемы и воздействий, используемых исследователем;
- плотность – пространственное распределение физической характеристики тела, которое требуется реконструировать с помощью системы;
- истинное изображение – изображение, в котором для любой точки пространства значение реконструированной плотности не зависит (в идеальном случае) от значений плотности вне окрестности этой точки, если окрестность – минимальный объем тела, разрешаемый системой.
Используя эти термины, определим компьютерную томографию как метод реконструкции истинного изображения распределения плотности с помощью определенных вычислительных операций над данными, полученными в результате прохождения воздействия через тело.
В табл. 8 для каждого вида воздействия приведены названия соответствующего метода компьютерной томографии, характеристика плотности, пространственное распределение которой реконструируется с помощью данного метода, и современное состояние развития метода. Как видно из таблицы, компьютерная томография является действительно универсальным методом медицинской интроскопии.
Практически все виды воздействий, применяемых в медицинской интроскопии, с большим или меньшим успехом используются для получения изображений методами компьютерной томографии. Каждый из методов компьютерной томографии независимо от вида воздействия и визуализируемой характеристики основан на фундаментальных методах реконструкции по проекциям, впервые разработанных Радоном еще в 1917 г.
Методы реконструкции изображения в компьютерной томографии. Проблема восстановления структуры многомерного объекта по совокупности его проекций в настоящее время решается многими методами [87], которые можно разбить на два класса – итерационные и аналитические. Проекция, в общем случае, – это отображение N-мерной функции в (N–I)-мерную путем ее интегрирования в заданном направлении. В основном все разработанные алгоритмы реконструкции предназначены для восстановления двухмерных объектов, так как для восстановления изображения во всем объеме трехмерный объект может быть аппроксимирован набором двухмерных сечений, если они расположены достаточно густо. Такая процедура оказывается более эффективной, так как существенно упрощает вычисления и требует меньшего объема памяти ЭВМ.
Итерационные методы реконструкции изображения используют аппроксимацию восстанавливаемого объекта массивом ячеек, с постоянной внутри ячейки плотностью. Распределение плотности ц (х, у) в сечении объекта ищется в виде квадратной матрицы из n столбцов и n строк элементарных ячеек.
Реконструкция осуществляется методом последовательных приближений, при котором выбирается произвольное начальное изображение, для него рассчитываются проекции, а затем в изображение вводятся поправки для лучшего согласования этих проекций с измеренными проекциями. Процедура повторяется до тех пор, пока не будет получена удовлетворительная сходимость. В зависимости от того, каков механизм ввода поправок и в какой последовательности они вводятся, в настоящее время имеется несколько алгоритмов итерационного восстановления. В алгебраическом методе восстановления (ART), примененном G. Haunsfield в первом варианте томографа, используется получевая коррекция, т. е. сначала вычисляется одна лучевая сумма, а по ней и с учетом измеренной лучевой суммы определяется поправка, которая вводится во все ячейки, входящие в состав данного луча. Операция последовательно повторяется для каждого луча. В методе одновременного итерационного восстановления (SIRT) используется коррекция по ячейкам, т. е. каждая итерация начинается с коррекции определенной ячейки всеми проходящими через нее лучами и проводится последовательно для каждой ячейки. В итерационном методе наименьших квадратов (ILST) используется одновременная коррекция по ячейкам. Сначала вычисляются все проекции по исходным значениям в ячейках, затем сравнением расчета с измерением определяются поправки для каждой ячейки и одновременно вводятся в каждую ячейку. На этом итерация заканчивается и начинается новая.
Несмотря на приближенный характер решений, итерационные методы позволяют реконструировать объект с нужной точностью при достаточном количестве итераций, но требуют больших затрат машинного времени.
Аналитические методы реконструкции в компьютерной томографии базируются на аппарате преобразования Фурье. Их разделяют на две группы: двухмерная реконструкция Фурье и обратная проекция с фильтрацией, при этом чаще всего используются фильтрация Фурье и фильтрация сверткой. Прежде чем перейти к описанию вышеперечисленных методов, разберем наиболее наглядный метод обратной проекции. В простейшем варианте этого метода плотность в любой точке сечения оценивается путем суммирования лучевых сумм для всех лучей, проходящих через эту точку. Восстановление производится путем обратного проецирования каждой проекции через плоскость, т. е. величина сигнала, которая соответствует данной лучевой сумме, присваивается всем точкам, образующим этот луч. После того как эта процедура проделана, для всех проекций получается приближенная аппроксимация исходного объекта. На рис. 62 показан результат восстановления точки (6-функции) методом обратной проекции. Результат восстановления – это многолучевая звезда, у которой точка – центр звезды представлена наиболее ярко, а яркость лучей убывает пропорционально расстоянию от центра. Таким образом, на окружающее пространство реконструированная точка накладывает фон, искажающий изображение.
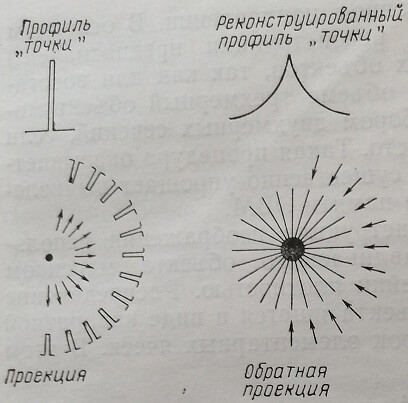
Рис. 62. Реконструкция точечного объекта методом обратной проекции
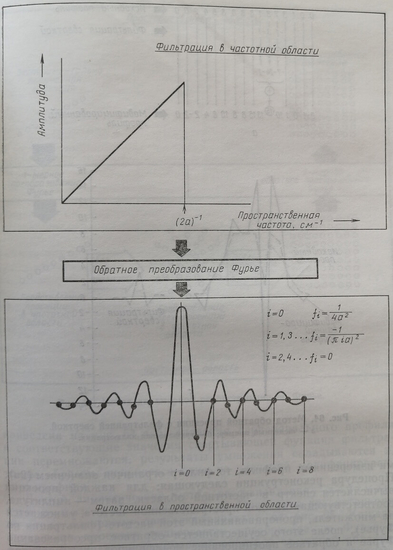
Использовать метод обратной проекции можно, если соответствующим образом модифицировать проекции перед обратным проецированием. Фон, искажающий восстановленное методом обратной проекции изображение, можно рассматривать как потерю информации об изображении в области высоких пространственных частот. Для того чтобы восстановить эту информацию и избавиться от фона, проекции перед операцией обратного проецирования модифицируются так, чтобы потеря пространственных частот компенсировалась в реконструированном изображении. Такую модификацию удобно проводить с использованием аппарата преобразования Фурье. Иллюстрация метода обратной проекции с фильтрацией по Фурье приведена на рис. 63. Так как в изображении не могут присутствовать пространственные частоты выше чем (2а)-1, где а – расстояние между двумя соседними отсчетами в частотной области.
Рис. 63. Метод обратной проекции с фильтрацией по Фурье преобразованию
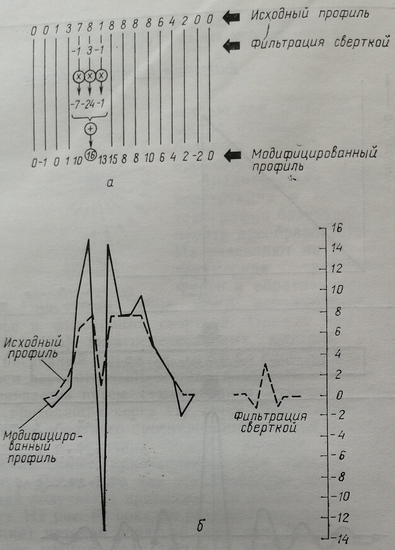
Процедура реконструкции следующая: для каждой проекции вычисляется спектр в частотной области, затем – амплитуда, соответствующая каждой пространственной частоте, умножается на множитель, пропорциональный этой частоте (фильтрация по Фурье), после этого осуществляется обратное преобразование Фурье и обратное проецирование модифицированной проекции на плоскость изображения. Для реализации этого алгоритма требуется соответствующая вычислительная техника для быстрого преобразования Фурье (БПФ-процессор). Фильтрация сверткой не требует преобразования в частотную область. Модификация проекции может осуществляться в пространственной области путем свертки исходной проекции с соответствующей свертывающей функцией фильтрации. Иллюстрация метода приведена на рис. 64, а, б. Значения первоначального профиля и соответствующие значения свертывающей функции фильтрации перемножаются, результаты умножения складываются и, таким образом, получается одно из значений модифицированного профиля.
Рис. 64. Метод обратной проекции с фильтрацией сверткой. а – численный пример; б – графическая иллюстрация
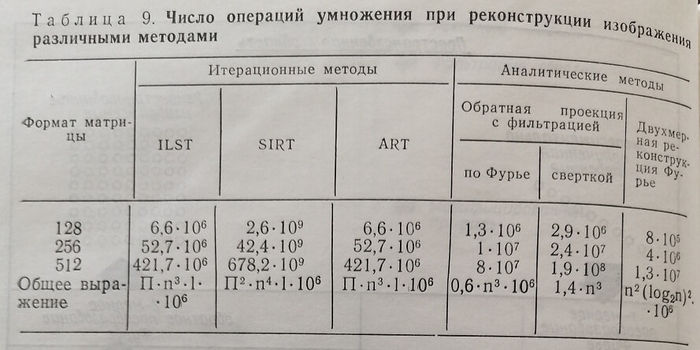
Другой аналитический метод восстановления – двухмерная реконструкция Фурье. Процедура реконструкции по этому алгоритму проиллюстрирована на рис. 65. Каждая измеренная проекция подвергается преобразованию Фурье и для нее вычисляется одномерный спектр в частотной области. Затем все проекции суммируются и проводится интерполяционный расчет всего массива при переходе от полярных к прямоугольным координатам в Фурье-области. После этого с помощью двухмерного обратного преобразования Фурье получают восстановленное изображение в пространственной области. Этот алгоритм также требует для реализации вычислительную технику для быстрого преобразования Фурье. В табл. 9 приведена сравнение различных методов реконструкции по количеству операций умножения для матриц изображения различного формата (1 – число итераций).
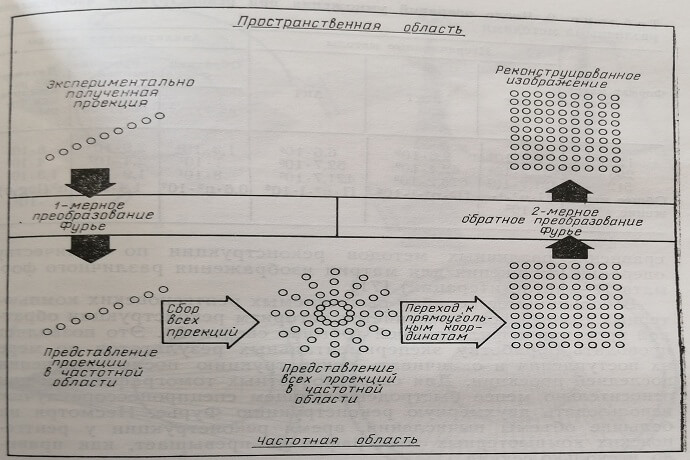
Рис. 65. Метод двухмерной реконструкции по Фурье
В большинстве серийно выпускаемых рентгеновских компьютерных томографов применяется алгоритм реконструкции обратной проекции с фильтрацией (обычно сверткой). Это позволяет проводить обработку экспериментальных результатов по мере их поступления и оканчивать реконструкцию после получения последней проекции. Для сверхскоростных томографов или при относительно менее быстродействующем спецпроцессоре лучше использовать двухмерную реконструкцию Фурье. Несмотря на большие объемы вычислений, время реконструкции у рентгеновских компьютерных томографов не превышает, как правило, несколько секунд.